Compressive sensing enables architectures
To perform JPEG, MPEG, and wavelet image compression, images are first digitized and a specific function used to compress them-in the case of JPEG compression a discrete cosine transform (DCT). Such compression reduces the bandwidth required for transmission and is widely used as the basis for image transmission in the broadcast industry.
“However,” says professor Richard Baraniuk of Rice University (Houston, TX, USA; www.ece.rice.edu), “although signal or image sampling is a linear process, any sparcity within the image is not taken into account.” At this year’s NIWeek (Austin, TX, USA; www.ni.com/niweek), Baraniuk presented a technique that combines image sensing and compression in which the signals or images can be simultaneously sampled and compressed at a greatly reduced rate. Known as compressive sensing, the method exploits the sparse nature of signal or image data.
“Many researchers are familiar with the Shannon-Nyquist sampling theory,” says Baraniuk. “This states that to perfectly reconstruct a continuous-time baseband signal from its samples, the signal must be band limited and the sampling frequency greater than twice the signal bandwidth. In many systems, data are then compressed, trading off signal representation complexity (bits) for some error (consider JPEG image compression in digital cameras, for example). Clearly, this is wasteful of valuable sensing resources.”
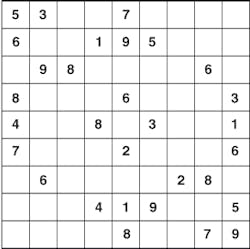
Compressive sensing can, perhaps, best be understood as analogous to the Sudoku logic-based number placement puzzle. Invented by the late Howard Garns in 1979, the aim of the puzzle is to fill a 9 × 9 grid so that each column, each row, and each of the nine 3 × 3 regions contains the digits from 1 to 9 (see Fig. 1). Although the person setting the puzzle only provides an incomplete grid, there is only one solution to the puzzle, found by inserting a unique number in a particular region and also in the horizontal and vertical columns.
“Now imagine that instead of a set of numbers, the two-dimensional array represents an image. Although there are missing data (the image is said to be sparse), there is only one result that can occur by interpreting these image data,” says Baraniuk. Indeed, when such image data are sparse, a condensed representation of the image can be acquired with little or no information loss. Thus, a typical CCD or CMOS camera need not read out all the information about an image scene but merely digitize a random sample of the image signal.
To simultaneously digitize and compress the image and then recover a complete image from these random samples, however, prior signal sparsity information must be known. “The number of measurements (M) that must be taken on a given image or signal,” says Baraniuk, “depends on the sparseness or compressibility (K) where K
While compressive image sampling is fairly straightforward, recovering the image data is more complex. “Unlike the Sudoku puzzle, where only one solution exists, a number of different solutions exist in the ill-posed inverse reconstruction of sampled images. Thus,” says Baraniuk, “given a matrix or image with a specific null space, the system must compute the best image fit.” This is best accomplished by mild over sampling of the signal such that the number of measurements required, M = cK Log (N/K).
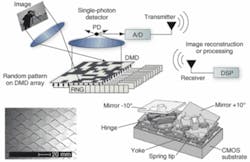
To demonstrate the capability of compressive imaging, Baraniuk and his colleagues have developed a digital camera that directly acquires random projections of a scene without first digitizing the pixels. The camera architecture employs a digital micromirror array from Texas Instruments (Dallas, TX, USA; www.ti.com) to optically calculate linear projections of the scene onto pseudorandom binary patterns (see Fig. 2).
The camera can obtain an image or video with a single detector while measuring the scene fewer times using a reduced number of pixels reflected from the micromirror. Since the camera relies on a single photon detector, it can also be adapted to image at wavelengths where conventional CCD and CMOS imagers are blind.
Others are also using compressive sensing in the development of imaging systems. At the Massachusetts Institute of Technology (Cambridge, MA, USA; www.mit.edu), Rob Fergus and his colleagues have developed a random lens camera that computes random sums using a random mirror (see Fig. 3). By using a CCD array, many random sums are acquired simultaneously by the camera’s CCD. Then compressive sensing is used to reconstruct a high-resolution image.