Using fuzzy logic in image processing
Andrew Wilson, Editor, [email protected]
Fuzzy set theory is an extension of conventional set theory that deals with the concept of partial truth. Originally introduced by Lotfi Zadeh of the University of California Berkeley (Berkeley, CA, USA) in 1965, fuzzy logic aims to model the vagueness and ambiguity in complex systems. In recent years the concept of fuzzy logic has been extended to image processing by Hamid Tizhoosh and others at the Pattern Analysis and Machine Intelligence (PAMI) research group at the University of Waterloo (Waterloo, ON, Canada).
“In many image processing applications, expert knowledge must be used for applications such as object recognition and scene analysis,” says Tizhoosh. “Fuzzy set theory and fuzzy logic provide powerful tools to represent and process human knowledge in form of fuzzy if-then rules. Many difficulties in image processing arise because the data, tasks, and results are uncertain. This uncertainty, however, is not always due to the randomness but to the inherent ambiguity and vagueness of image data. Beside randomness-which can be managed by probability theory-other kinds of imperfection in image processing include grayness ambiguity, geometrical fuzziness, and vague knowledge of image features.
“These problems are fuzzy in nature. The questions whether a pixel should become darker or brighter than it already is, where the boundary between two image segments is, and discriminating whether a tree is present in a scene are examples of where fuzzy approaches can be used,” says Tizhoosh.
“The idea of fuzzy sets is simple and natural,” he continues. “In some images, for example, it may be necessary to define a set of gray levels that share the property of being dark.”
In classical set theory, a threshold such as the gray level 100 has to be set. But since the darkness of a particular pixel is a matter of degree, a fuzzy set (or subset to be precise) can model this property much better. To define this subset, two thresholds, say gray levels 50 and 150 are required. Then all the gray levels that are less than 50 are full member of the set and all gray levels greater than 150 are not member of the set. Gray levels between 50 and 150, however, have a partial membership in the set.
To perform image processing using fuzzy logic, three stages must occur. First image fuzzification is used to modify the membership values of a specific data set or image. After the image data are transformed from gray-level plane to the membership plane using fuzzifi cation, appropriate fuzzy techniques modify the membership values. This can be a fuzzy clustering, a fuzzy rule-based approach, or a fuzzy integration approach. Decoding of the results, called defuzzification, then results in an output image. “The main power of fuzzy image processing is in the modification of the fuzzy membership values,” Tizhoosh says.
In image processing, some objective quality criteria are usually used to ascertain the results of such processing. For example, an image may be “good” if it possesses a low amount of fuzziness indicating high contrast. Human beings, however, may not perceive these results as good because such a judgment is subjective. This distinction between objectivity and subjectivity is the first major problem in human machine-interaction. Another difficulty occurs because different people may judge image quality differently. This inter-individual difference is also primarily due to the human subjectivity.
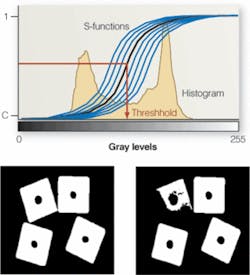
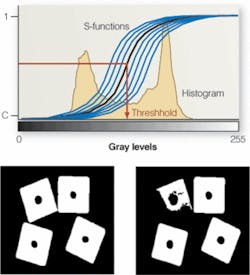
“There are many classical thresholding techniques used in image processing,” says Tizhoosh, “and recently the concept of image fuzziness has been used to develop new thresholding techniques.” For example, a standard S membership function can be moved pixel by pixel over the existing range of gray levels and in each position, a measure of fuzziness calculated. The position with a minimum amount of fuzziness can be regarded as a suitable threshold (see figure). A more advanced approach uses type II fuzzy sets; these are fuzzy sets whose membership function does not deliver a number but another membership function.
Fuzzy logic has found numerous commercial applications in machine vision and image processing. One software package, Fuzzy Decision Desk from Fuzzy Logik Systeme (Dortmund, Germany) is a rule-based fuzzy decision module, which, in combination with Common Vision Blox from Stemmer Imaging (Puchheim, Germany; www.stemmer-imaging.com) performs intuitive image analysis by means of rules formulated with linguistic terms as big, medium, and small that describe specific quality aspects of any criteria using a relatively small number of rules.
Using the program, the developer can create a fuzzy project in which the variables, terms, and rules necessary for decision-making can be edited with graphic support. A program-integrated fuzzy decision component controls the inference behavior. Specific quality criteria are defined in the form of linguistic variables, and results presented as a relevant statement in the form of crisp values.
For embedded applications, the Fuzzy Inference Development Environment (FIDE) from Aptronix (Santa Clara, CA, USA) can also be used to describe many concepts that are commonly used in object description and detection, such as “exactly collinear,” “roughly collinear,” and “almost like a circle.” Supplied with a set of code generators, FIDE automatically generates fuzzy inference algorithms in Java code, ANSI C code, MatLab M file, and assembly code for a variety of microcontrollers. According to Aptronix, due to the direct mapping from fuzzy logic statement set to machine instruction set of the target microcontroller, the size of the assembly code generated is smaller than handwritten assembly programs, and the time needed to execute code is much shorter.
Other Websites on this topic
Aptronix
www.aptronix.com
Fuzzy Logik Systeme
www.fuzzy.de
Stemmer Imaging
www.stemmer-imaging.de
University of California, Berkeley
www.berkeley.edu
University of Waterloo
http://pami.uwaterloo.ca/tizhoosh/fi p.htm
Wikipedia
en.wikipedia.org/wiki/Fuzzy_logic
Wolfram Research
www.wolfram.com/news/fuzzylogic2.html