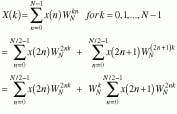FFT chips quicken image recognition in vision systems
FFT chips quicken image recognition in vision systems
By Andrew Wilson, Editor at Large
Many digital image-processing systems, especially for advanced military and medical imaging applications, require fast pattern matching for precision image-recognition results. Military target-recognition systems, for example, might require the accurate location of a given target template in an image. Similarly, in medical imaging systems, biological cells of a specific type may need to be located in slides containing thousands of such cells. In many of these systems, where high speed is critical, optical correlators have been used to perform the forward and inverse fast Fourier transforms (FFTs) needed in pattern matching (see Vision Systems Design, July 1998, p. 50).
Although optical correlators are extremely fast and often capable of processing images at 200-frame/s rates, these devices sometimes have limited resolution due to the spatial light modulators (SLMs) used in such designs. Fortunately, the reduction in line geometry of VLSI circuits has allowed semiconductor vendors to implement the FFT algorithm on single integrated circuits (ICs). In such implementations, computational speeds on the order of 50 ms for 1024-point complex FFTs are not uncommon
FFTs in silicon
Pattern-matching systems built around FFT integrated circuits are similar to their optical counterparts except that FFT and inverse-FFT (IFFT) processing are performed digitally, not optically (see Fig. 1). In such systems, pattern matching is accomplished by performing a two-dimensional (2-D) FFT of the target scene and multiplying this FFT with a precomputed template representing the object to be recognized. After an inverse FFT of the resulting multiplication is performed, the location of the best match is determined.
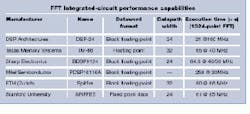
Performing FFT and IFFT processing is a highly computational task, requiring IC architectures to be built with pipelined multiplier-accumulator stages. To address this need, DSP Architectures (Vancouver, WA), Mitel Semiconductor (Kanata, Ontario, Canada), Sharp Microelectronics Technology (Camas, WA), Texas Memory Systems (Houston, TX), and others have implemented a number of single-chip ICs (see table on p. 38).
Whereas nearly all commercially available devices implement a block floating-point function to increase computational dynamic range, one part, the TM-66 from Texas Memory Systems, is a true 32-bit floating-point device.
Discrete implementations
Whether block or floating point, most FFT processors rapidly perform a discrete Fourier transform (DFT) using pipelined architectures of multipliers and accumulators. To make these processors more efficient, the algorithms originally developed by James Cooley and John Tukey1 are implemented to divide the original DFT computation into smaller DFT computation stages.
For instance, in Cooley`s and Tukey`s Algorithm 11 (see Fig. 2), an N-point DFT is represented by two N/2-point DFTs. If N is a power of two, partitioning can be applied iteratively until the two-point DFT is reached. This so-called decimation-in-time (DIT) algorithm is based around a radix-2 butterfly stage (see Fig. 2), in which two input points are computed to two output points. If the data are complex, each radix-2 butterfly requires one complex multiplication and two complex additions for every butterfly cycle. This process is equivalent to four real multiplications and four real additions for every cycle. Therefore, for an N-point FFT, each stage needs N/2-radix butterflies for a total of (N/2) log 2N radix-2 butterflies.
To perform the FFT on large data sets of 1024 points, for example, designers of FFT ICs must increase the data throughput to the chip. They do so by observing that different orders of radices such as radix-4 and radix-16 can increase the number of samples to 4 and 16 points, respectively. Because the radix-16 transform can be implemented as two radix-4 pipelines or four radix-2 butterfly stages, designers can partition the DFT algorithm in several ways.
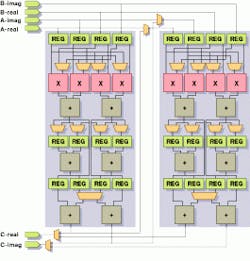
In device architectures such as the Texas Memory Systems TM-66, a radix-16 stage is implemented as two radix-4 pipelines, allowing two complex words to be input each cycle (see Fig. 3). In each of its two pipelines, the TM-66 device can perform a complex multiplication in the first stage followed by complex additions in stages two and three. And, once the pipeline is primed, this IC can produce a complex result every cycle for the radix-16 transform.
Like the TM-66, the LH9124 device from Sharp Microelectronics has a data path optimized for computation of the radix-4 butterfly. Unlike the TM-66 but like DSP Architectures` DSP-24 processor, Sharp`s device is a 24-bit block floating-point device. By using a block floating-point method, both devices infuse systems built around them with some of the enormous dynamic range of true floating-point functionality without incorporating much on-chip logic. According to Mike Fleming, president of DSP Architectures and chief architect of both the Sharp 9124 and DSP-24 processors, 95% of the market for such ICs only demands 24-bit block floating-point precision.
Silicon size
Architectural trade-offs can also reduce the size of silicon in FFT platforms. In the design of the Sharp 9124 chip, Fleming optimized the architecture of the device for the radix-4 butterfly by allowing six multiplications and 11 additions per cycle. Here, recalls Fleming, the architecture of such devices must be input/output (I/O) balanced. If each radix-4 butterfly requires 16 real multiplications, then a radix-16 transform architecture needs 96 multiplications. If the device is required to sample data at 100 MHz, then 10 ns is required to bring data to the device from off-chip. Once the data arrive, the IC needs 16 cycles to perform the 96 multiplications with six on-board multipliers.
"Eight floating-point multipliers are used in the TM-66 to give the device better symmetry and to optimize it for very-high-end applications," says Fleming, "even though in a radix-4 transform, only three complex multiplications are required."
Claimed as the highest-performance 24-bit block floating-point device available, the DSP-24 architecture is called a unified, scaleable transform-based approach by Fleming. On-board the device, twenty 24-bit multipliers are arranged in a proprietary architecture that can perform a 1024-point complex FFT in two passes, for a continuous sampling rate of 50 MHz.
Speeding the FFT
Because the FFT architecture is structured, currently available FFT ICs can be designed in cascaded or parallel architectures to speed the transform. Cascading four DSP-24s, for example, yields a 100-million-samples-per-second (MSPS) complex FFT capable of performing a 1024 ¥ 1024 2-D FFT in 20 ms. At DSP Architectures, Fleming has developed such a processor around a multichip module (MCM) with four DSP-24 die connected back to back.
"In a two-phase concurrent process, phase one runs all die concurrently with the top two chips performing 1024 of the required 1024-point complex FFTs, and the result is stored in an external 1 million-point RAM," explains Fleming. "While this is taking place, the bottom two chips in the MCM are taking the results from a previous pass and also performing 1024 of the required 1024-point complex FFTs for the final output." In the second phase of this process, the chip pairs swap working memories, allowing real-time processing in a seamless pipelined fashion.
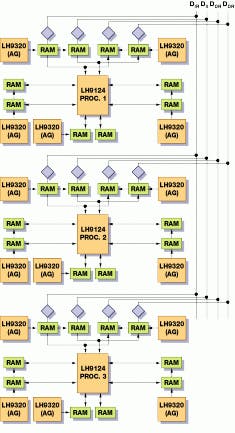
An alternate way to improve the throughput for the FFT is to use parallel processing. The merit of the parallel approach is that each processor can run an independent job or algorithm. Such a parallel design is based around the Sharp LH9124 device (see Fig. 4). Built as a common parallel bus system with three processors, this device can implement a 4096-point FFT as three stages of radix-16.
"Because each 9124 IC can process the 4096-point FFT in 312 ms," says Fleming, "a three-chip system based around such an architecture will take approximately 104 ms--a speedup of three times."
Board-level support
With such high performance available from single-chip solutions, third-party board-level vendors are now offering products based on these devices. Catalina Research (Colorado Springs, CO), PCM Systems Corp. (Dublin, CA), Sundance Multiprocessor Technology (Waterside, Chesham, England), Interactive Circuits & System (Gloucester, Ontario, Canada), and Valley Technologies (Tamaqua, PA) all offer products based around dedicated FFT devices.
While many of these boards are offered for the VME bus, some companies offer PCI- and TIM-based add-in modules. For the design of its CRCV1MX0 5.5-giga operations per second (GOPs) board, Catalina Research chose the Eurocard 9U format to host six cascaded LH9124 devices capable of continuously performing a 1024-point FFT in 25.6 ms. In operation, the board can execute up to 1 million-point FFTs using 24-bit block floating-point arithmetic.
Sharp`s LH9124 device also finds its way onto the ICS-2200 board from Interactive Circuits and Systems (ICS). Available in single (ICS-2200S) and dual (ICS-2200D) VME versions, the ICS-2200D includes a second DSP device on a daughtercard. Providing up to 320 million operations per second (MOPs) and 640 MOPs sustained computing power, this board can process up to 2048 input channels simultaneously.
FFTs and DSPs
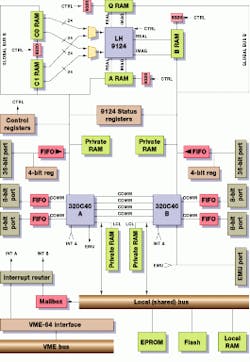
Although companies such as Catalina Research and ICS have developed dedicated processing boards, other companies such as PCM Systems (Dublin, CA) have developed more-conventional DSP-based boards using dedicated FFT processors to speed FFT acceleration. Such a product, the DSP-449 from PCM Systems combines a Sharp LH9124 block floating-point vector processor with two Texas Instruments TMS320C40 scalar DSP processors to form a VME-based board suitable for high-speed FFT-based DSP applications. In this approach, vector and scalar processors are interconnected through shared memory to minimize data movement while performing array operations with both processor types (see Fig. 5). The Sharp LH9124 device can perform FFT operations more than ten times faster than scalar processors, and the TMS320C40 units can perform search, decision, and branching routines concurrently with the LH9124 device`s vector operations.
Like PCM Systems, Sundance Multiprocessor Technology also combined a DSP IC (the TI C44), with an LH9124 butterfly chip in the design of its SMT311, a Texas Instruments Module (TIM) subsystem capable of performing a two-dimensional 512 ¥ 512 real FFT in 31 ms and a 1024-point complex FFT in 64.6 ms.
Valley Technologies (VT) has coupled vector processors such as the DSP Architectures DSP-24 and the Sharp LH-9124 with wideband I/O options, including RACEway, FPDP, C40 communications port, PCI, and VME interfaces. As one of the first companies to integrate DSP Architectures DSP-24 processors, Valley Technologies offers the VT-5000 series of VME baseboards that is centered around the VT-5100 DSP core processing module. This module is placed on a 3 ¥ 5-in. circuit card containing the DSP Architectures 100-MHz DSP-24 FFT processor and a MMU-24 memory-management unit. The VT-5280, a VME baseboard, can support up to two VT-5100 processor modules and two VT-11XX input/output modules.
With Fourier-transform ICs available as single-die MCM solutions implemented on boards with various form factors, systems integrators can easily increase the speed of medical and military vision systems that require fast image-correlation speeds. Better yet, as semiconductor geometries become smaller and clock speeds increase, the speed of performing such image correlations in silicon may soon approach those only currently available with optical systems. When this happens, the role of the optical-based correlator will decrease as digital systems capable of processing high-resolution images at ultrafast speeds replace them.
FIGURE 1. Pattern-matching systems built around digital FFT ICs devices are similar to their optical counterparts except that both FFT and inverse FFT processing are performed digitally. In these systems, pattern matching is accomplished by performing a 2-D FFT of the target scene and multiplying the result with a pre-computed FFT template of the object to be recognized. Performing an inverse FFT of the result determines the location of the object.
FIGURE 2. In Cooley`s and Tukey`s Algorithm 11 (top), an N-point discrete Fourier transform (DFT) is represented by two N/2-point DFTs. If N is a power of two, this partitioning can be iteratively applied until the two-point DFT is reached. This decimation-in-time algorithm is based around a radix-2 butterfly stage (bottom). In this stage, two input points are computed to two output points. If the data presented are complex, then each radix-2 butterfly requires one complex multiplication and two complex additions every butterfly cycle, the equivalent of four real multiplications and two real additions.
FIGURE 3. The Texas Memory Systems TM-66 IC architecture implements a radix-16 butterfly as two radix-4 operations. In each of its two pipelines, the TM-66 can perform a complex multiplication in the first stage, followed by complex additions in stages two and three. Once the pipeline is primed, the IC produces a complex result every cycle.
FIGURE 4. In many image-recognition applications, FFT devices can be used in a parallel-processing architecture to improve throughput. Three Sharp LH9124 processors are linked via a common parallel to implement a 4096-point FFT as three stages of radix-16.
FIGURE 5. In the design of the DSP-449 from PCM Systems (Dublin, CA), a Sharp LH9124 block floating-point vector processor is combined with two Texas Instruments` TMS320C40 scalar DSP processors on a VME-based board. Vector and scalar processors are interconnected through shared memory to minimize data movement while performing array operations with both processor types.
reference
1. J. W. Cooley, and J. W. Tukey, "An Algorithm for the Machine Calculation of Complex Fourier Series," Mathematics of Computation (1965).