Geometric pattern-matching targets pick-and-place systems
Andrew Wilson, Editor, [email protected]
Recognizing different-sized parts that may be occluded or that may be placed at random orientations under different light conditions is often accomplished with geometric pattern-matching techniques. For the vision-guided robotics industry, this method has proven most useful in pick-and-place systems, in which a camera-guided robot needs to pick randomly oriented parts from a bin and properly orient them on a linear or rotary conveyor. Companies such as Adept Technology (Livermore, CA, USA; www.adept.com), Cognex (Natick, MA, USA; www.cognex.com), Dalsa Coreco (St.-Laurent, QC, Canada; www.imaging.com), and Matrox Imaging (Dorval, QC, Canada; www.matrox.com/imaging) offer this functionality as part of their machine-vision software toolkits.
Now, Stemmer Imaging (Puchheim, Germany; www.stemmer-imaging.de) has joined these companies with its own geometric pattern-matching tool called Shapefinder II. As part of the company’s Common Vision Blox software package, the tool presents the developer with an easily trained, subpixel accurate interface.
“In developing a system that is invariant to translation, rotation, and scaling of parts,” says Volker Gimple, senior software-development engineer at Stemmer, “the system developer must first train the system using a known good part.” As part of this training, the developer may define a reference point and reference angle of the object. In recognizing a door key, for example, this reference point may be the center part of the handle within the key.
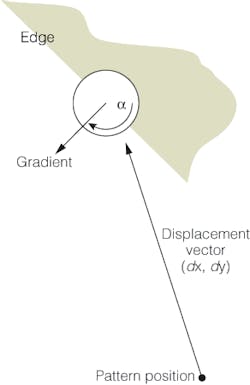
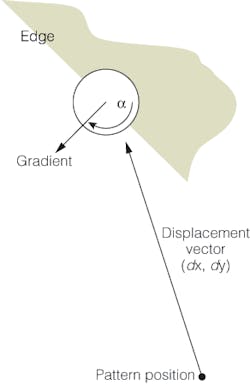
“This reference point is required,” says Gimple, “since the geometric pattern-analysis algorithm uses a generalized Hough transform to compute the point gradient density along lines in the image data space.” In the example of door-key recognition, the gradient changes along the shaft of the key will all be very similar.
However, at other points, such as the tip of the key, these gradient changes will be more pronounced-and these regions normally provide the most useful information for geometric pattern recognition. To properly perform geometric pattern-matching, an image classifier is needed. Using the position of each of these features, their gradient direction and their position relative to the reference point-in other words a vector and an angle-can be computed (see figure).
“In the simplest case,” says Gimple, “a number of these vectors and angles can build a classifier that is invariant to translation, rotation, and scaling.” However, because some images from machine-vision systems can be very large, this classification process can be compute-intensive. To increase the speed of this computation, images can be downscaled with a Laplacian pyramid technique that uses a convolution filter to reduce the number of pixels at each scale by a factor of two.
“Although downscaling techniques can be helpful,” says Gimple, “it is important that the system still recognize enough pronounced gradient changes at a number of points in the image.” By performing image classification on the downscaled image, pattern-matching occurs much faster. However, because this classification has been performed on a downscaled image, the position of each part and its angle of rotation may only be accurate to within a few pixels and a few degrees, respectively.
To overcome this limitation, classification data from a downscaled known good sample are first correlated with classification data from the downscaled classification data from the part being examined. Once correlated, the section of the image that contains the possible matched can be upscaled, and classification data computed and compared with data from the original known good sample.
“With this process,” says Gimple, “it is possible to obtain a theoretical 0.006-pixel and 0.07° accuracy. Of course, such subpixel accuracy must be contextually placed. Simple analog frame grabbers still in use today feature pixel jitter of about ±0.1 pixels,” says Gimple, “making such claims by any software manufacturer redundant. So it is always important to keep an eye on the whole vision system and not only an isolated component to get the best performance out of it.”