Model-based design speeds image processing
According to Jerry Krasner of Embedded Market Forecasters (Framingham, MA, USA; www.embedded-forecast.com), the complexities and uncertainties surrounding embedded software developments continue to escalate development costs and frequently challenge product “windows of opportunity.” Engineering costs associated with design delays are further exacerbated by the failure of most embedded designs to approximate expectations.
“To address these difficulties and complexities”, he says “model-based design provides a single design environment that enables developers to use a single model of their entire system for data analysis, model visualization, testing and validation, and ultimately product deployment, with or without automatic code generation.”
In June 2004, The MathWorks (Natick, MA, USA; www.mathworks.com) introduced the latest version of its Simulink software for simulation and embedded system development. Designed to bring model-based design to complex projects encompassing large models and multiple design teams, new capabilities of the package allow engineers to model, simulate, and implement real-time systems and components. In July, The MathWorks released the Video and Image Processing Blockset, a library of graphical block-based components for the Simulink simulation environment specifically dedicated to development of embedded video and imaging systems.
To demonstrate one example of the capabilities of the Video and Image Processing Blockset, Don Orofino, manager of signal processing development at The MathWorks, has developed a video template tracking and motion stabilization demonstration in the Simulink environment. The demonstration system is currently bundled with the latest release of the Video and Image Processing Blockset.
“Several steps are required to implement a video-tracking and motion-stabilization system,” says Orofino. “These include estimating a target position from a template, computing interframe motion, compensating for that motion, and updating the matching template.” To accomplish this, the system can be presented with an image of the initial target template region and a region within the image to search for that target.
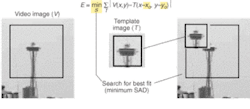
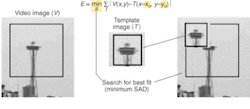
“One of the simplest ways to match the template image with the target image is to use a block-matching algorithm such as the Sum of Absolute Differences (SAD).” In this algorithm, the template image is shifted across the incoming video image in a defined search region. Pixel values of the template image are subtracted from corresponding pixel values within the incoming image and added together: the smallest sum then represents the best match.
“Although SAD provides motion estimates with integer pixel coordinates, it is still an approximation to the true target motion,” says Orofino. “To reduce video-stabilization jitter and accumulated errors over time, a fractional pixel estimate of the target position is used,” he says. This requires the use of sub-pixel estimation. In the demonstration system developed by The MathWorks, a two-dimensional quadratic interpolation was used to find the sub-pixel minimum over a 3 × 3 neighborhood. This is accomplished using matrix algebra components from the Blockset. Once this minimum is computed, the absolute (x, y) offset of the target position between frames is determined. “Although we have only compensated for translational motion using this technique,” says Orofino, “it could easily be extended to encompass rotational motion by computing the angle change of two interframe targets.”
Once the target position has been determined from the template and the inter-frame motion computed, motion compensation can be accomplished. The two dimensional offset (x.y) provides the necessary feedback that allows incoming frames to be translated (motion compensated) to the correct degree (see figure on p. 15). This is accomplished by a 2-D interpolation block, where the quality of the interpolation result is selectable by the user based on their requirements for quality of result versus computational overhead. “Because this is a closed feedback loop,” says Orofino, “it can “wander off” when specific data sets are used or parameters set incorrectly. This demonstration model is a convenient starting point for the practicing image-processing engineer to evaluate such trade-offs while developing an embedded video-based application.”
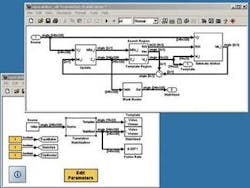
To estimate the position of a target within an image, The MathWork’s video stabilization system uses the SAD block-matching algorithm to search for best possible fits (top). Implemented using the Video and Image Processing Toolbox-now part of the company’s Simulink software-the system (left) consists of a template tracker block (far right), a motion estimator block (middle), and a motion compensation block (far left). Because the software is hierarchical, clicking on each block allows developers to interrogate the underlying blocks of the system to the sub-block and code level. Here, parameters can be set using menu boxes and, if required, the underlying code modified.
Running on a Pentium-based PC, the algorithm is capable of both real-time target tracking and motion estimation, even during desktop simulation. According to Orofino, engineers could refine this demonstration model by offering rotation compensation. This would require computing the angle change of motion between two frames and will initially be accomplished by finding the angle between the coordinates of two tracked objects with known relationship and using these data to compensate for rotation. In addition, leveraging the matrix algebra capabilities of Simulink, engineers could minimize the size of the predicted motion region using Kalman adaptive filter blocks, depending on their application requirements.
Because The MathWorks now supports fixed-point mathematics in MATLAB, the company’s interactive environment for algorithm development, designers can implement and verify such systems built with fixed-point hardware and software. A number of development tools are available for this purpose. These include Texas Instruments (TI; Dallas, TX, USA; www.ti.com) Code Composer Studio for verification, debugging, visualizing, and validating TI DSP software by establishing real-time bidirectional data transfer links among MATLAB and TI’s software development environment, and TI DSP hardware. Simulink users can also write algorithms using a subset of the MATLAB language and automatically generate C code using The MathWorks’ Real-Time Workshop.