HOW THE APPLICATION OF fuzzy logic SHARPENS IMAGE ANALYSIS
HOW THE APPLICATION OF fuzzy logic SHARPENS IMAGE ANALYSIS
By Barry Phillips, Contributing Editor
Fuzzy logic--a mathematical technique for representing and manipulating degrees of uncertainty in data sets--emerged in 1965 with the publication of Fuzzy Sets by Lotfi Zadeh, now director of the Initiative on Soft Computing at the University of California at Berkeley. Developers are now reaping the rewards by applying fuzzy logic techniques in very complex systems such as pattern recognition.
"Fuzzy logic can be used in image-contrast enhancement, edge detection, image segmentation, image-understanding systems, and rule-based systems for medical diagnosis and pattern recognition," says James C. Bezdek, editor of IEEE Transactions on Fuzzy Systems and professor of computer science at the University of West Florida (Pensacola, FL).
"In imaging applications, there are 10,000 scientific papers on fuzzy logic and a dozen different applications. There is also a choice of approaches that use optimization-type models or knowledge-based systems,"says Bezdek.
At the National Severe Storms Laboratory (Norman, OK), researchers are using an optimization-type fuzzy model to analyze uncertainties associated in weather prediction (see "Radar and fuzzy logic predict severe weather pattern," p. 36). With current methods there is a lot of uncertainty associated with the 3-D radar signature. A new fuzzy model tests severe radar signatures using fuzzy models that analyze several aspects of the radar`s profile, including its 3-D structure, vertical height, reflectivity range, and proximity to mesocyclones. In contrast, knowledge-based fuzzy models are typically used in complex systems that have multiple models, multiple layers of abstraction and multiple decision making steps, such as pattern recognition problems.
Fuzzy language
For those unfamiliar with fuzzy sets and fuzzy logic, the terminology can be confusing. Traditional image-processing techniques use `crisp values` and `crisp sets.` A crisp approach to thresholding converts gray-level images to binary images based on an absolute gray-level threshold value. Each pixel is then given a new value based on the threshold value.
Using a fuzzy gray-scale model, each pixel is defined using a fuzzy variable such as `very gray,` `somewhat gray,` and `a little gray.` Logical comparisons that operate on these `fuzzy variables` are called `fuzzy rules.` Fuzzy edge detection might compare the fuzzy gray-level values of each pixel with the fuzzy gray levels of pixels that occur in the surrounding area. Sets of objects, or pixels, that meet a set of fuzzy rules, known as a `membership function,` are called members of a `fuzzy set.`
Unfortunately, it is difficult to know when fuzzy models or more conventional modeling approaches are appropriate. Image segmentation is a case in point. There are many ways to perform image segmentation, and any one of hundreds of crisp, fuzzy, or statistical clustering methods can be used. "All of these techniques can be called upon to segment images, and for a particular image one of them is probably better than the other. But from image to image, you do not know which method will be best," says Bezdek.
"The best approach is to use whatever additional information you have, such as the distributional source of sensor data, to preselect models that have a good chance of working," says Bezdek. "But, once this is done, be prepared to start over, because in image processing and pattern recognition, everything is ultimately driven by the data and not by preconceived notions about what the data should be like." Bezdek asserts that it is customary to advocate fuzzy models in cases where there is a clear element of nonstatistical uncertainty.
Medical imaging
Fuzzy systems are becoming popular in edge detection for magnetic resonance imaging (MRI) and digitized x-rays. A recent survey prepared by Bezdek, A geometric approach to edge detection, cites 60 different references on the use of fuzzy sets in segmentation of medical images. In magnetic resonance images of the brain, fuzzy clustering methods identify regions that are bone, fat, gray cells, spinal fluid, and tumor tissue.
Bezdek has also used a fuzzy-reasoning-based edge detector to improve tissue discrimination in digitized mammograms (see "Fuzzy logic gives software developers the edge," p. 38).
Fuzzy logic is also refining digital angiography, a procedure that visualizes vessels and cavities of the heart. Several methods have been devised for estimating the ventricle contour, such as Bayesian-model-based segmentation. Now researcher Medina Rubén at the University of the Andes (Merida, Venezuela) is using fuzzy-based segmentation to estimate left ventricular contours of the heart (see Fig. 1).
First, a fuzzy classification algorithm provides a fuzzy partition of the image. Then a fuzzy membership function is computed for each pixel that classifies it as belonging to the ventricle or image background. The image is then partitioned by classifying pixels according to image attributes. The algorithm can analyze several attributes and the fuzzy set partition expanded to include other regions or tissue classes.
Fuzzy word recognition
Another major application of fuzzy logic is handwriting recognition, a special case of pattern recognition. Handwritten-word recognition involves matching a binary digital image of a handwritten word to a dictionary or lexicon. Given a digital image of a handwritten word and a lexicon, the task is to find the word in the lexicon that best matches the image.
What makes handwriting recognition tough is that handwriting varies so widely. The challenge is to overcome the ambiguity and uncertainty of characters present in the handwritten word (see Fig. 2). The letter `J` often looks like `U,` and a lower-case `g` often gets mistaken for the number `9.` Many handwriting-recognition methods segment an image into subimages before applying algorithms for recognition. This process introduces even more ambiguities. Conversely, a correct segmentation of an image can include several subimages that contain legitimate characters but that do not look like the actual characters.
"The question is how do you represent that uncertainty within a program," says Paul Gader, assistant professor of computer science at the University of Missouri at Columbia. "Fuzzy sets can represent this ambiguity and uncertainty," he says.
But isolated character recognition cannot take into account information regarding spatial and lexical compatibility of adjacent character images. And successful handwritten-word recognition algorithms cannot rely on simply isolating and recognizing individual characters. "Local information representing possible locations and identities of character images must be evaluated within the context of the word to arrive at the best interpretation of the image,"says Gader.
Gader`s heuristic computer programs for handwriting recognition combine traditional crisp-image segmentation, fuzzy character recognition, and high-level word-matching algorithms. The fuzzy character-classification module is just one element of a larger, complex fuzzy knowledge-based system. The program uses `fuzzy integrals` to combine information from the handwritten character and word-recognition modules.
Fuzzy integrals are a nonlinear way of aggregating information from multiple sources that include character memberships, the relationships between characters, and information at the word level. "Fuzzy integrals allow you to combine information from disjoint information sources so that the whole is not equal to the sum of the parts. Unlike a probability measure, it`s not additive,"says Gader. Fuzzy sets are ideal for complex intelligent systems such as computer vision systems because they naturally embody a "principle of least commitment," asserts Gader. According to the principle, decision-making should be delayed as long as possible.
FIGURE 1. Fuzzy-based segmentation is used to estimate the left ventricle contours in a heart image. First, a fuzzy membership function classifies parts of the image as belonging to the ventricle or image background. The image is then partitioned by classifying pixels according to image attributes. The algorithm can analyze several attributes and the fuzzy set partition expanded to include other regions or tissue classes.
FIGURE 2. In handwritten-word recognition, isolated character recognition does not provide information about adjacent character images, and word recognition algorithms cannot rely on isolating individual characters. Fuzzy integrals combine data from multiple sources to overcome this problem.
Radar and fuzzy logic predict severe weather patterns
-- Lak Lakshmanan
National Severe Storms Laboratory
Norman, OK
(405) 366-0530
E-mail: [email protected]
Researchers are developing fuzzy-logic algorithms to detect and predict hail storms and tornadoes based on radar signatures. Doppler weather radar detects backscattering of radar waves and wind velocity within thunderstorms by scanning a range of 250 km every five to six minutes at elevation angles ranging from 0.5 to 19.5. This yields a set of images at various elevation angles.
But problems exist when using radar to predict weather. The farther away storms are from radar, the coarser sampling becomes. And, because radar is tilted from the Earth`s surface and the surface itself is curved, it cannot sample low parts of storms far away. Uncertainty also exists when collecting radar signatures because storms move and evolve while being scanned. As weather prediction is complex, radar signatures are not sufficient--prediction algorithms must also include the storm`s direction, evolution, and vertical structure.
By using fuzzy logic, the prediction model can incorporate uncertainty using rules based on how far the updraft is from the radar, even if the rules are not completely satisfied. Fuzzy logic combines rules such as: "If the region has a low minimum reflectivity AND is to the right of the storm THEN this is where an updraft is expected to be." The degree to which this statement is satisfied is used with other rules to finally classify the radar signature.
In radar reflectivity of a Lubbock, TX, storm at successively higher elevation angles, the two circled areas are possible updraft regions. The region on the left is not an updraft, although it has the associated radar signature. The circled region at right in each figure is an updraft.
Fuzzy logic gives mammogreaphy the edge
-- James C. Bezdek
Department of Computer Science
University of West Florida
Pensacola, FL 32514
E-mail: [email protected]
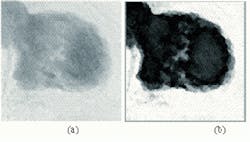
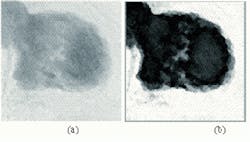
Developers of image-analysis systems should consider fuzzy reasoning as a means of improving the results of conventional techniques. Fuzzy models are ideal for analyzing medical images because boundaries between tissue classes are not well defined. For example, neither human beings nor computers can determine where to mark transitions from malignant to nonmalignant cells in a breast-cancer tumor. In such applications, fuzzy pattern recognition can detect edges in digital mammograms that correspond to pertinent anatomical features. In addition, the mammograms can be better tailored to display specific features within such images.
To detect edges in digital mammograms, a sequence of conditioning, feature extraction, blending, and scaling is performed. First, conditioning functions improve the quality of the raw sensor image. Here, a special form of histogram equalization is used because in digital mammograms 20% of the pixels may be black. Next, feature-extraction functions estimate edge features. To accomplish this, Sobel filtering is performed using a 3 ¥ 3 kernal. Blending functions then gather information about specific edge vectors, such as the Euclidean norm. Scaling functions then adjust the intensities in the blended image so that the edge image has the desired gray-level range.
Two blending functions, one using the Euclidean norm and one using a Takagi-Sugeno-based fuzzy system are compared in the figure. Figure a shows a histogram-equalized digitized mammogram. Figure b shows an edge image produced by blending the Sobel features with the Takagi-Sugeno-based fuzzy system. Figure c shows an image obtained by blending the same features with the Euclidean norm.
Figures b and c show very different characteristics. While images such as b are useful for characterization and detection of internal structures such as mass lesions, the reduced intensities in c are useful for operations such as boundary detection.
Figure c is the only image that can be produced by blending the Sobel features with the Euclidean norm. In contrast, alteration of a single parameter in the Takagi-Sugeno model enables it to produce images like both 1b and 1c. As a benefit, the fuzzy model provides developers with greater flexibility to tailor characteristics of the displayed image than the Sobel/Euclidean approach.