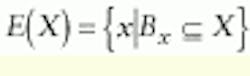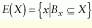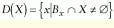Understanding mathematical morphology
Understanding mathematical morphology
Bruno Lay
Mathematical-morphology-software operations are widely used to solve complex imaging applications involving shape recognition, image enhancement, image compression, and image analysis, among others. This month`s column discusses the concepts of erosion and dilation, homotopic operations, skeleton, and some basic morphological measurements.
Compared to other software techniques such as convolution, filtering, and edge detection, mathematical-morphology operations concentrate on the task of reducing imaging information. This is needed and applied, in general, to remove much of the original image data and to retain only relevant information. For example, if you are interested only in large, circular objects in the image, successive morphological operators can be applied to remove all "nonrelevant" objects such as small, noncircular ones.
All morphological operators can be derived from a basic operation called erosion. A dilation, therefore, is the complement of an erosion. A skeleton is derived from an operation named `hit or miss,` which is a combination of erosion and dilation. These operator names explain why some developers speak of `image algebra` when referring to mathematical morphology and other related imaging techniques.
In the early development of morphology, just a single morphological operation, erosion, and a geometrical shape-structuring element were available. Structuring elements are characterized by a well-defined shape (such as line, segment, or ball), size, and origin.
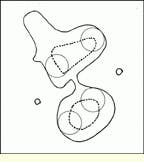
The erosion (E) operation consists of a set X and a structuring element B. The result of an erosion operation is a set of points x from X where B is centered on x and is completely included in X (see Fig. 1):
The erosion process causes all isolated points and small objects to disappear. It also disconnects nearby objects, smoothes the object boundary from the inside, and reduces the size of the original objects. Changing the shape of the structuring element affects the result of the erosion. Note that large structuring elements can be decomposed into smaller ones. For example, performing an erosion with a square of size 10 is equivalent to doing 10 successive erosions with a square of size one. This explains why morphological processes often involve hundreds of basic operations and why very fast hardware or a clever software implementation of basic morphological operators must be used.
Usually, for an image, an erosion is performed with a square structuring element that is moved over all points in the image. For all image points whose value is 1 and whose eight neighbors are also 1 (when a 3*3 square is considered as the structuring element, with nine points), the output value of the point is set to 1; otherwise, it is set to 0.
A dilation (D), which is the complement of an erosion, affects the background of the objects in the same way that erosion affects the shape of the foreground (set X). In other words, the complement of the erosion of an object (X) with a structuring element (B) is equivalent to the dilation (D) of the background of the object (complement of X; see Fig. 2):
Combining erosion and dilation yields two new operations: opening and closing. An opening is an erosion followed by a dilation; a closing is a dilation followed by an erosion. An opening removes small objects, disconnects nearby objects, and smoothes the object boundary from the inside. It does not shrink shapes as erosion does. A closing fills holes inside objects, connects nearby objects, and smoothes the boundary from the outside. Again, it does not expand shapes as dilation does.
Opening and closing are called idempotent operations. This means that repeating the same opening yields the same result. The notion of idempotence is extremely useful in morphology as it is used to stop an iterative process.
The result of an opening is always contained within the original objects. And the original objects are always completely contained in the result of a closing. Opening and closing are often used to filter an image by removing small objects or artifacts and keeping the larger ones.
The skeleton operator is based on a `thinning` operation. Skeleton is defined as the medial axis, or the centers of all the maximal disks that can fit into an object. It can also be described as the propagation of `fire` from the edges of an object. A fire operator stops propagating when it comes into contact with other fire operators. The collection of extinction points is the skeleton. There are different ways to compute the skeleton of an image. It can be obtained from the distance function or from `thinning.` Thinning can result in a skeleton, the boundary of a binary object, or the centroid of all objects. It can also remove small branches on a skeleton. The actual results depend on the shape of the structuring element used in the transformation, the number of times the structuring element is applied, and the different orientations of the structuring element. Note that skeleton is a homotopic operation, which means that if there are 10 objects in the original image, then there are also 10 objects after skeletonization. In other words, it preserves the topology of the objects.
Common applications of skeleton involve thinning the blood vessels in an image to determine their thickness, thinning printed characters to aid in their recognition, and detecting characteristic points in an object such as intersections and crossings. Moreover, character recognition can be performed after skeletonization by looking at loops, triple points, end points, and the distance from the skeleton to the nearest border.
Geodesy is the fundamental principle behind operations such as `hole fill,` which fills holes into objects; `border kill,` which eliminates objects touching the border; and `reconstruction,` which reconstructs objects from markers. It can be defined as an iterative process for a morphological operator with intermediate and final results constrained to the boundary of a given object.
For example, starting from a binary image with the three objects described previously, consider as markers the triple points of the skeleton. Reconstruction is equivalent to performing successive dilations of the markers and intersecting at each stage of the process with the original binary image. Starting with the markers, objects containing these markers are totally reconstructed after the process.
Geodesic operations are commonly used in morphology. Special morphological hardware often has an additional output arithmetic logic unit to perform an intersection on the output of any morphological operation.
In addition to image-processing operators, which generate an image from an image, there are many morphological techniques for measuring shapes in an image--the "morph." Originally, these measurements were used to quantify metal samples in material science. Today, they are used in a broad range of applications including medical analysis and quality control.
Shape parameters, such as the perimeter, the intercept numbers, the number of entries in an object in given directions, the connectivity or Euler`s number, and the shape factor defined from the area and the perimeter, are all computed using structuring elements and counting the number of occurrences. More-complex measurements such as the geodesic diameter are also derived from morphological techniques.
FIGURE 1. When an erosion (E) is performed on an original set X with a ball used as the structuring element
the eroded set E (X) is obtained by looking at all the points of X where the ball is totally included in X. As a result, the ball is moved inside the set X, and all the points where the ball is totally included in the original set X are part of the eroded set.
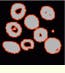
FIGURE 2. Starting with a binary image, a dilation with a 3*3 square structuring element is performed.
The small holes are filled after dilation, and the nearby objects are connected. The red areas indicate what the process added. The structuring element is moved outside the set X, and all the points that the structuring element hits in the original set X belong to the dilation.
BRUNO LAY is president of ADCIS SA, 14200 Herouville Saint-Clair, France; e-mail: bruno@ aai.com.