Understanding image enhancement (Part 2)
Understanding image enhancement (Part 2)
PETER EGGLESTON
A special class of enhancement operators modifies the gray-level histogram of data. A histogram is a graph that shows the number of pixels at each gray level in the histogram but discards spatial information. These operators redistribute the gray-level assignments so that the histogram becomes a predetermined shape. When the histogram is leveled, or evenly distributed, this process is called histogram equalization.
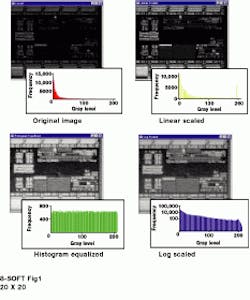
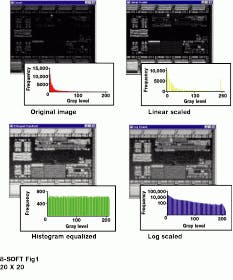
To create a flat histogram, the redistribution of the pixel values at one gray level often needs to be mapped to several adjacent gray values. This method is called "one-to-many mapping." If this method is not implemented in a random fashion with regard to the spatial location of the pixels, enhancement might be biased in certain portions of the image (see Fig. 1).
Contrast enhancement can be implemented so that it operates globally on the entire image in the same manner, or locally, so that it applies differing amounts of compensation to each pixel, or areas of pixels, in the image. The easiest way to implement a local contrast-enhancement algorithm is to calculate the gray-level minimum and maximum values in a local neighborhood about each pixel and use these values to construct a gray-level mapping function that is unique to each pixel. This approach is sometimes also termed locally adaptive enhancement, as the enhancement parameters adapt to the local data characteristics.
Some contrast-enhancement techniques, such as stretching, might cause clipping or saturation at both ends of the scale. Poorly implemented scaling functions do not compensate for this problem and, therefore, cause the ends of the scale to "wrap" around to the other end of the intensity range. Also, these techniques can`t create new data. That is, they cannot fill in the holes in the stretched intensity space.
Because images are discrete integer representations of data and contrast-enhancement techniques are continuous analog functions, the output gray-level values are quantized to the nearest integer values, causing gaps in the output image`s gray-scale. This condition, sometimes called "dithering," might not be detrimental to viewing the image, but could cause problems in later applications of filtering and segmentation techniques on the data.
Feature enhancement
Some imaging applications call for the enhancement of certain features in the image data, such as edges or color. Color enhancement can be achieved by applying filters to the data to boost or suppress certain color components or hues. This enhancement might be done by applying differing amounts of scaling to each color band, or by modifying the hue and saturation components of the image. In each case, operators are needed that can operate separately on each individual red-green-blue color component. Or, processing can be done on alternate color space transformations of the data, such as hue, saturation, and intensity.
Color enhancement is often used to correct for the characteristics of the imaging system, such as those imparted by cameras, film, scanners, printers, and displays. However, color correction is a complex task, and few software programs can solve this problem. A thorough understanding of color space is needed to devise algorithms that operate adequately on color data (see Fig. 2).
Edge enhancement is used to "sharpen up," or improve, the contrast about the edges of an image. Because of the discrete nature of imaging sensors, an image edge might be smeared due to undersampling. That is, if a pixel samples across the boundary of an object, it will represent a value that is comprised of partial background and partial object, resulting in a "fuzzy" edge. Sensor or object motion and poor optical systems might also cause the object boundary to blur. This blurring can be interpreted as an attenuation of high frequencies. Or, it can be interpreted as an integration of the values about a sampled location. Sharpening an image can therefore be accomplished by boosting or emphasizing its high-frequency components, or by creating new components by differentiating the values about an edge.
The simplest method of edge enhancement involves the use of filtering techniques to accentuate the high-frequency components of an image (see Vision Systems Design, June 1998, p. 19). An alternative approach is to create a derivative image and then add a portion of this image back to the original. Because images are not continuous functions, difference functions such as the Laplacian operator are used to create these derivatives. For example, convolving the following Laplacian kernel with an image
0 -1 0 or -1 -1 -1
-1 4 -1 -1 9 -1
0 -1 0 -1 -1 -1
produces another image that shows the rate of change, or edge strength, between adjacent pixels. Brighter areas represent edges, and dimmer areas indicate locations of uniformity.
Adding the Laplacian-generated image from the original exaggerates the profile of the edge (see Fig. 3). The amount of edge enhancement can be controlled by scaling the Laplacian image before the adding process. The resulting effect is known as "ringing" for analog signals, a process whereby the signal undershoots the value at the low side of the edge and overshoots the value at the top end. Many televisions include this functionality in their hardware to increase the apparent sharpness of the televised signal.
An alternative to the Laplacian approach is to create a difference image by subtracting a blurred image from the original. Blurring can be accomplished via a low-pass filter such as the convolution of an image with a kernel whose elements are all "1s," or through the use of Gaussian averaging by a pyramid filter (see Vision Systems Design, June 1998, p. 42). In essence, this approach is equivalent to using a Laplacian filter with more support area (larger neighborhoods). The advantage of this approach is that it finds fewer but more obvious edges. This effect reduces the emphasis of noise in the image.
Morphological gradients can also be used to perform edge enhancement. This class of operators performs morphological edge detection by subtracting the eroded image from the dilated image. Different structuring elements lead to different gradients, such as oriented edge detection if line-segment structuring elements are used. Like Laplacian-based edge sharpening, the gradient image is added back into the original signal to enhance the edges.
A major disadvantage of edge-enhancement techniques is that they enhance the noise as well as the edges of the objects of interest in the image. Applying a noise-reduction operator first, such as a median filter, can reduce some noise effects.
Choosing the correct image-enhancement techniques for use in imaging applications is aided by a thorough understanding of their effects and limitations. The results achieved depend on the characteristics of a particular image, and their appropriateness can be determined through interactive experimentation. Implementing the proper software tools supports the rapid exploration of these and other image operators. As with all imaging-processing techniques, users must be cognizant of any artifacts the enhancement operator introduces, as they might significantly affect later processing steps.
Peter Eggleston
Part 1 of "Understanding image enhancement" was published in Vision Systems Design, July 1998.
FIGURE 1. In some applications, contrast enhancement is used to correct nonlinearity in image-acquisition systems. In other applications, it is used to compact some parts of the gray scale while expanding other parts to improve viewing or processing. The original image (upper left) has a disproportionate amount of information in the lowest section of its 0 to 255 gray-level range, as seen in the corresponding histogram. Linear scaling improves the image viewability somewhat (upper right), but it does not make full use of the dynamic intensity range and introduces clipping or saturation. Logarithmic scaling (lower right) and histogram equalization (lower left) work well for this image, but histogram equalization can introduce artifacts in the data.
FIGURE 2. Color correction in images is complicated, but many software packages can compensate for nonlinearities in the scanning and output processes. Note the differences in the original image (left) and the color-corrected version (right).
PETER EGGLESTON is senior director of business development, Imaging Products Division, Amerinex Applied Imaging Inc., Amherst, MA; e-mail: [email protected].