INTEGRATION INSIGHTS - Into the Depths

Depth of field is crucial to maximizing performance in camera systems

Gregory Hollows

Low-cost, high-resolution cameras certainly have allowed machine-vision and image-processing systems to become more cost effective, but this increased resolution has presented system integrators with new challenges. To fully leverage the capability of these products, developers must understand the capabilities of cameras and the optics that must be used to maximize their resolution.

One of the greatest challenges facing system developers is determining how to properly match lenses with high-performance cameras and how to establish the resolving power of lens/camera combinations using test targets. Key to deploying camera systems in machine-vision equipment is understanding how high resolution can be maintained over the application's required depth of field.

Often confused with depth of focus, the depth of field (DOF) of an imaging system is the range of distances in front of and beyond the best focus position of the system at which objects are imaged with acceptable sharpness. Quite often in high-resolution applications there is the desire to maintain near-pixel-limited resolution over a large DOF. Unfortunately, system integrators and end users are finding that this is almost impossible and tradeoffs are unavoidable.

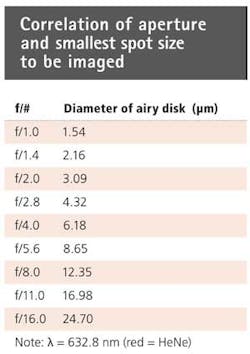
In simple terms, there is a direct correlation between the smallest achievable spot size (image detail) that a lens can produce and the aperture (f/#) of the lens (see table). When the aperture of the lens is largest, the f/# is smallest. Conversely, as one reduces the aperture size, the f/# increases. As the f/# increases, the spot size becomes larger and the resolution decreases. Because high-resolution sensors generally feature very small pixels—usually less than 4 µm—this presents a problem when trying to maximize resolution. By comparing the pixel sizes found in today's sensors with the smallest achievable spot size at any given aperture, it can be seen that low apertures (f/#s) are required to theoretically maximize these high-resolution sensors.

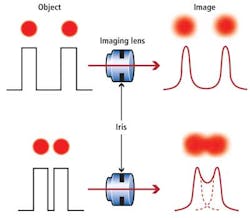
Figure 1 shows what occurs when any resolution increases, even those at the theoretical limits. For a fixed-aperture setting, the overlapping information reduces the height difference between the peaks and valleys of the signals. This change in amplitude is the contrast level at that resolution. If resolution increases (the spots move close enough together), eventually there is no valley between the signals and the spots. Thus, they can no longer be discerned and there is no contrast. When the aperture is closed (the f/# is increased) to obtain better DOF, the spots representing the achievable resolution get larger (see table). This causes the spots to overlap, leading to lost contrast. Generally an aperture of f/6 or lower is required to achieve good/usable contrast levels (see "Matching Lenses and Sensors," Vision Systems Design, March 2009).

FIGURE 1. As resolution of an image increases, spots created are moved closer together; constructive interference occurs between the different spots that have been imaged, thus reducing resolution. Notice that the overlapping spots still have a trough between them, allowing them to still be resolved but at with greatly reduced contrast. As the aperture (f/#) is increased to achieve a higher depth of field (DOF), increased constructive interference leads to a reduction of both resolution and contrast that can be obtained at best focus.

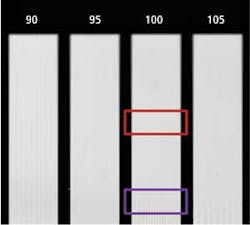
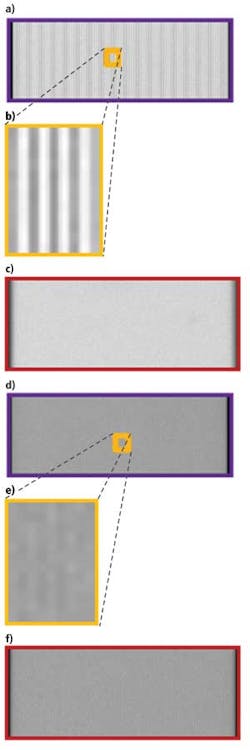
Figure 2 shows a target that is made up of groups of black and white lines of varying widths (or frequencies). By having different frequencies on one target, different resolutions can be evaluated simultaneously. This test target—a Ronchi ruling—is slanted at a 20° angle in relation to the imaging system to create areas of best focus (shown in purple) and a position closer to the lens system that is not in best focus (shown in red). Examining these multiple line frequencies at 35 and 100 line pairs/mm, in this example, at different apertures highlights the effect on the system's DOF. The frequencies were used with pixel-limited resolution in mind, with consideration for the specific lens' magnification.

The group of lines imaged in Fig. 3 is near the pixel-limited resolution of the system. Each line consists of one pixel on a black line and the adjacent pixel on a white line. In Fig. 4, the lines are at approximately three times the width of those in Fig. 3, and consist of about three pixels on each black and each white line.

Figure 3a and 3b show that there is resolvable detail using an f/6 lens setting at best focus. However, at the area under inspection above best focus (Fig. 3c), no detail can be resolved. In the lower-resolution images of Fig. 4a and 4b, there is resolvable detail at both depths using an f/6 lens setting.

When greater DOF is required using lower-resolution sensors (that create images similar to those in Fig. 4) the aperture of the lens can be increased. By operating the camera system with an aperture setting of f/12 or f/16, the resolution at best focus can be maintained well enough to effectively achieve the application's objectives.

FIGURES 3 and 4 (left and right, respectively). Close-up sections of two different frequencies of a Ronchi ruling test target taken by a camera show the results of imaging a pixel-limited-resolution system taken with a lens aperture setting of f/6 (Fig. 3a, 3b, and 3c) and one at one-third the resolution (Fig. 4a and 4b), also at f/6. While increasing the aperture to f/12 in both images results in an increased DOF in low-resolution images (Fig. 4c and 4d), the pixel-limited images of Fig. 3d, 3e, and 3f have no resolvable detail associated with them.

By examining the high- and low-resolution images of Fig. 3 and 4, one can see the effects of closing the aperture on performance. Using low-resolution images (shown in Fig. 4c and 4d), closing the aperture (increasing the f/#) greatly increases the ability to resolve the lines above best focus (Fig. 4d) while maintaining a reasonably strong image at best focus (Fig. 4c).

Unfortunately, this is not the case for the high-resolution images shown in Fig. 3. Using an aperture setting of f/12, it can be seen that all of the images for Fig. 3d, 3e, and 3f have no resolvable detail associated with them. This is because increasing the f/# on a pixel-limited system results in an increased spot size, thus leading to decreased image contrast. Simply put, the system has been pushed beyond the physical limits of the optics to resolve details that small. It should be noted that the same effects are occurring at lower resolution. However, at one-third the resolution, there is a much higher amount of contrast at the start; there remains a significant amount of contrast in the system after the aperture (f/#) change. Thus, the tradeoff for DOF is not as detrimental. Eventually, if the f/# is increased enough, the same results would be encountered at the lower resolution as well.

Specifying system performance has always been critical to success in machine vision and imaging. In the past, most systems, although exacting, did not usually approach limitations imposed by the laws of physics. Today, this is no longer the case. These limitations and need to be understood to create realistic expectations about what imaging systems can achieve.

Key to deploying camera systems is understanding how high resolution can be maintained over the application's required depth of field.

Gregory Hollows is director, machine vision solutions, at Edmund Optics (Barrington, NJ, USA).